5.1. RECTA TANGENTE Y RECTA NORMAL A UNA CURVA EN UN PUNTO. CURVAS ORTOGONALES
Una recta tangente a una curva en un punto, es una recta que al pasar por dicho punto y que en dicho punto tiene la misma pendiente de la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión.
Sea  una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
 una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
La tangente es la posición límite de la recta secante (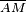 ) (el segmento
) (el segmento 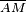 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
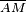 ) (el segmento
) (el segmento 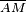 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
Si  representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 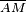 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
 representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 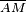 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
Donde 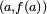 son las coordenadas del punto
son las coordenadas del punto  y
y 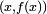 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
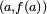 son las coordenadas del punto
son las coordenadas del punto  y
y 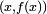 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
Es, por definición, f '(a), la derivada de f en a.
La ecuación de la tangente es  :
:
 :
:
La recta ortogonal a la tangente 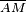 que pasa por el punto
que pasa por el punto 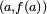 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
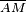 que pasa por el punto
que pasa por el punto 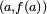 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
suponiendo claro está que 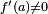 . Si
. Si 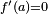 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.
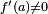 . Si
. Si 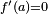 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.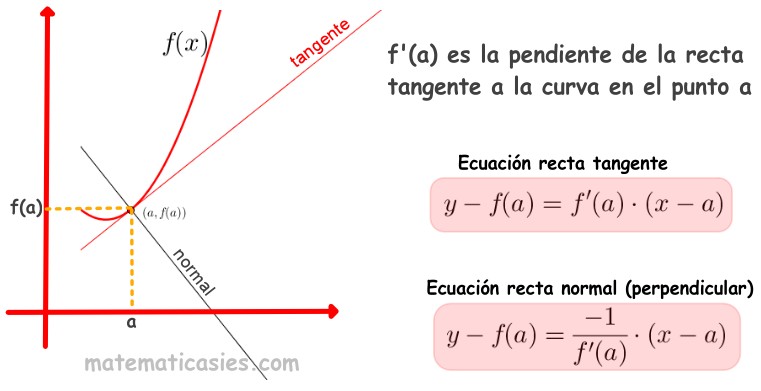
5.2. TEOREMA DE ROLLE, TEOREMA DE LAGRANGE O TEOREMA DEL VALOR MEDIO DEL CALCULO DIFERENCIAL.
La derivada de una función en un punto es la pendiente de la recta tangente a la función en ese punto.
§
La ecuación de la recta tangente a una función en el punto A( a , f ( a ) ) viene dada por la expresión: y – f ( a ) = f ’ ( a ) [ x – a ]
§
Dos rectas paralelas tienen la misma pendiente.
§
Si en un punto de la gráfica de una función se produce un cambio brusco de dirección ( “un pico” o “punto anguloso”), la función no es derivable en dicho punto.
TEOREMA DE ROLLE
Si f es una función continua en [ a , b ], derivable en ( a , b ) y además f ( a ) = f ( b ), entonces existe al menos un punto c Î ( a , b ) en el que f ’ ( c ) = 0.
2.1 Interpretación geométrica
Si se cumplen las hipótesis del teorema, existe al menos un punto c Î ( a , b ) en el que su recta tangente es paralela al eje de abscisas (es decir, es la recta y = f ( c ) ).
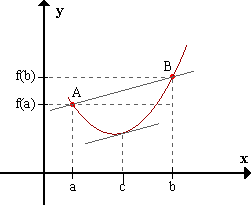
TEOREMA DEL VALOR MEDIO ( TEOREMA DE LAGRANGE)
Si f es una función continua en [ a , b ] y derivable en ( a , b ), entonces existe al menos un punto cÎ(a,b) en el que f ’ (c) = [ f ( b ) – f ( a ) ] / ( b – a ).
3.1 Interpretación geométrica
Si se cumplen las hipótesis del teorema, existe al menos un punto c Î ( a , b ) en el que su recta tangente es paralela al segmento determinado por los puntos A( a , f ( a ) ) y B( b , f ( b ) )
TEOREMA DEL VALOR MEDIO GENERALIZADO (TEOREMA DE CAUCHY)
Si f y g son dos funciones continuas en [ a , b ] y derivables en ( a , b ), entonces existe al menos un punto c Î ( a , b ) en el que se verifica: f ’ ( c ) [ g ( b ) – g ( a ) ] = g ’ ( c ) [ f ( b ) – f ( a ) ].
Es inmediato comprobar que el teorema del valor medio es un caso particular del teorema del valor medio generalizado. Para ello, basta tomar la función g ( x ) = x.

5.3. FUNCIÓN CRECIENTE Y DEPENDIENTE. MÁXIMOS U MÍNIMOS DE FUNCIÓN. CRITERIO DE LA PRIMERA DERIVADA.
Función creciente y Función decreciente
· Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x1 y x2, con la condición x1 £x2, se verifica que
f( x1 ) < f( x2 ).
Se dice estrictamente creciente si de x1 < x2 se deduce que f(x1) < f(x2).
· Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x1 y x2, que cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).
Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la función se dice estrictamente decreciente.
Máximos y mínimos de una función
Se dice que una función tiene un valor máximo en el punto v, cuando el valor de f(v) es mayor que el valor en cualquiera de los puntos vecinos.
Del mismo modo, cuando el valor es menor que el valor en sus puntos vecinos, entonces ese valor se convierte en el valor mínimo de la función.

Criterio de la primera derivada para máximos y mínimos
5.4. ANÁLISIS DE LA VARIACIÓN DE FUNCIONES.
En función de variación acotada, también conocido como BV función, es un numero real con valores de función cuya variación total está limitado (finito):
la gráfica de una función con esta propiedad se comporta bien en un sentido preciso.
Para una función continua de una sola variable, por ser de variación acotada significa que la distancia a lo largo de la dirección de la yEjes, dejando de lado la contribución del movimiento a lo largo de x Ejes, que recorre un punto movimiento a lo largo de la gráfica tiene un valor finito.
Para una función continua de varias variables, el significado de la definición es la misma, excepto por el hecho de que la trayectoria continua que se considera que no puede ser todo el gráfico de la función dada (que es un hipersuperficie en este caso), pero puede ser cada intersección de la propia gráfica con un hiperplano (en el caso de funciones de dos variables, una plano) paralelo a un fijo xEjes y al y Ejes.
Funciones de variación acotada son precisamente aquellos respecto de los cuales uno puede encontrar en las integrales de Riemann-Stieltjes todas las funciones continuas.
Otra caracterización de los estados que las funciones de variación acotada tienen es que encuentran que en un intervalo cerrado son exactamente los f que se puede escribir como una diferencia g − h, donde ambos g y h están limitados monótono.
En el caso de varias variables, en función f definido en un subconjunto abierto Q de Rn se dice que la variación acotada si su de distribución de derivados es un recurso finito del vector.
Uno de los aspectos más importantes de las funciones de variación acotada es que forman una álgebra de funciones discontinuas cuya primera derivada existe casi en todas partes:
debido a este hecho, se puede y con frecuencia se utilizan para definir soluciones generalizadas de problemas no lineales implican funcionales, ordinaria y ecuaciones diferenciales parciales en las matemáticas, la física y de ingeniería.
Teniendo en cuenta el problema de la multiplicación de las distribuciones o más en general el problema de la definición general de las operaciones no lineales en funciones generalizadas, función de variación acotada son los más pequeños y en la álgebra tiene que estar integrada en todos los espacios de funciones generalizadas preservar el resultado de multiplicación.
Análisis de la Variación de la Función
Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.
La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como
Donde S es el conjunto acotado
La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x).
Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:
1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).
2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.
Por ejemplo, la función g(r) = c es una función de variación acotada constante en el intervalo [x, y]. | g (ri) – g (ri - 1)| = 0 por cada partición del conjunto [a, b]. Por tanto, V (g, [x, y]) = 0.
3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso
a). g es una función de variación acotada en el intervalo [x, y].
b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].
c). cg es también una función BV en el conjunto [x, y].
d). g + f y g –f son BV en el conjunto [x, y]
e). gf es también BV en el conjunto [x, y].°°°°°°°
Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.
Del mismo modo, todas las funciones totalmente continuas son de naturaleza BV, sin embargo, no es necesario que todas las funciones continuas BV deban ser totalmente continuas.
La función f puede ser considerada como BV en el conjunto [x, y] si, la derivada de f se encuentra acotada en [x, y]. Además, cuando dos funciones variación acotada se multiplican entre sí, entonces la resultante es también una función de variación acotada.
Hay algunas propiedades básicas que son seguidas por las Funciones de Variación Acotada:
1) Las Funciones de Variación Acotada pueden tener discontinuidad de primer tipo, es decir, discontinuidad de salto.
| |||||
5.5 CALCULO DE APROXIMACIONES USANDO LA DIFERENCIAL
Hasta ahora se ha usado para la derivada de una función y con respecto a x, la notación de Leibnitz, dx/dy, como un símbolo y no como el cociente del símbolo dy (diferencial de a variable y) entre dx (diferencial de la variable x).
Se define en esta sección el concepto de la diferencial, que nos permite representar la derivada como un cociente y hallar el valor aproximado de la variación de una función alrededor de un punto.
La definición esta motivada por el siguiente razonamiento geométrico.
Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) (fig. (a)).
Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas
cuyos ejes dx y dy son paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen
y en consecuencia, su ecuación es bastante simple, a saber: dy = mdx, donde m es la
pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antíguo,
esto es m = f ’(x), se tiene entonces:
dy = f ’(x) dx
Lo anterior nos permite dar la definición formal de las diferencial.
Definición:
i. Se llama diferencial de la variable independiente x, denotada por dx, al
incremento ∆ x ; esto es dx = ∆ x .
ii. Si y = f (x) es una función derivable de x, la diferencial de y en el punto x,
denotada dy, se define como dy = f ' ( x ) ∆ x , o también,
dy = f ' ( x ) dx . Interpretación geométrica de la diferencial
Sea f una función derivable en x. En el triángulo P0RQ, se tiene: RQ = m.∆x ,
en donde m es la pendiente de la recta tangente a la curva en P0 (fig. (b)), y por tanto,
m = f ’(x0).
Así que: RQ = f ' ( x )∆ x = dy
0
Además, ( ) ( ) 0 0
∆ y = f x + ∆ x − f x (2)
Se puede observar entonces que:
∆ y : es el incremento en y medido sobre la curva; y,
dy : es el incremento en y medido sobre la recta tangente
Observaciones:
i. Si la ecuación y = f (x) corresponde a una línea recta, entonces dy = ∆ y para cualquier x del dominio.
ii. Puesto que dy = f ' ( x ) dx , si dx ≠ 0 , entonces al dividir ambos
miembros de la última igualdad por dx, se tiene: f ' (x)
dx
dy
= y se puede de esta forma interpretar la derivada de una función como el cociente de dos diferenciales.
iii. De acuerdo con la observación ii. todas las reglas de diferenciales se deducen de
las reglas de derivación (R.D.1.- R.D.16., sección ), multiplicando ambos
miembros de estas últimas por dx.
En la tabla siguiente aparecen las principales reglas de diferenciales deducidas de las
correspondientes reglas de derivación.
5.6 Problemas de optimización y problemas de tasas relacionadas
La optimización se refiere al tipo de problema que se ocupa de la determinación de la forma más apropiada para realizar cierta tarea. Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función. Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc. La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.
Estos problemas son diferentes a los problemas utilizados para encontrar los valores mínimos o máximos locales. Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo. Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local. El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.
Puede haber casos, donde el mínimo o máximo global no existe para una función. En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.









No hay comentarios:
Publicar un comentario